Category Archives: Uncategorized

Left4Dead tarzı Glow efekti

Posted on by

Oynamış olanlar neden bahsettiğimi biliyordur herhalde, oynamamışlarda kesinlikle denemesini öneririm.

Buradaki glow efektini directx üzerinde shader kullanarak yapmaya karar vermiştim. Sonuç yeterli gibi oldu.

test

Kullanması oldukça kolay. Kütüphanemizi yüklüyoruz. Effect i hazırlamak icin
void setupEffect(LPDIRECT3DDEVICE9 d3ddev, int w, int h);
fonksiyonu cağırılıyor. w ve h ekran boyutları oluyor.

Daha sonradan da
void drawGlowMesh(ID3DXMesh* mesh, D3DXVECTOR3 color);
ile mesh i color ile ekrana çiziyoruz.

Kullanabilmek icin bir kac seye ihtiyacımız var. d3ddev olusturulurken back buffer boyutlarını vermek zorundayız.
d3dpp.BackBufferHeight = SCREEN_HEIGHT;
d3dpp.BackBufferWidth = SCREEN_WIDTH;

Ayrıca stencil buffer destekleyen bir depth&stencil format kullanmalıyız. En çok kullanılan D3DFMT_D24S8 sanırım.

Son olarakta alpha blending açık olmalı.

.h ve .fx dosyamız

Ayrıca şu linkteki örnek üzerine ekledim. main.cpp örnek teki kod. kendi eklediğim ve değiştirdiğim satırlar //*** ile comment lendi ve açıklama yazıldı.

Örnek program (Adı postprocess olduğuna bakmayın, üşendim şimdi düzeltmeye =))

Collision Detection Üzerine

Posted on by

Biraz internette bulduğum bir collision detection algoritması üzerine bahsedeceğim. Şu sitede tanıştım kendisi ile

http://spiritking.tripod.com/cdtut.htm

Algoritma hareket eden insanı bir silindir olarak düşünüyor. Mantık olarak çok güzel düşünülmüş, performansıda gayet iyi gibi duruyor. Lakin sitedeki implementation biraz kusurlu olmuş ve algoritmanın biraz eksiği var gibi.

Collision detection için gerekli olan verilerimiz, kamera koordinatı, silindirin alt ve üst sınırlarının y koordinatları ve bir de silindirimizin yarı çapı. Ayrıca polygonlarımızın koordinatları, normal leri lazım olacak.

Şu resmi bir inceleyelim. (Yukarıdaki sayfada olduğu gibi benim programımda da y ekseni yukarısı olarak tanımlanmış)

collision1

Yukarıdaki resimde 3 tane polygonumuz var. Kamerada silindir ile gösterilmiş. En sağdaki polygon silindir ile collision yapmış gibi duruyor (daha kolay anlaşılması için o üçgeni hafif eğimli bir duvar gibi düşünün bizde üzerine doğru yürümüşüz) Sahnenin z yönünde bir kesini görüyoruz. Collision detectionun ilk aşaması silindirin alt ve üst yüzeylerinden geçen 2 tane düzlem düşünün. Bütün polygonları bu iki düzlem arasında kalan kısımlarını kullanıyoruz. Mesela soldaki polygon un hem üstünden hem altından kesmişiz ve sonuçta silindirin yükseklik sınırlarında kalan bir beşgen ortaya çıkmış.  Ortadaki polygon tamamı iki düzlem arasında kalmış, o yüzden bir kesintiye uğramıyor. Sağdakininde sadece alt kısmı kesilmiş ve gene ortaya bir üçgen çıkmış.(eğer bir polygon bu iki düzlemin tamamen ters taraflarında ise tamamen göz ardı edilecekti)

Ortadaki resim sadece polygonların kesildikten sonraki halini gösteriyor. Görebileceğiniz gibi kestiğimiz kısımların collision yapabilmesi imkansızdı, sadece bu parçalar collision ihtimaline sahip.

Burada kesme işleminin nasıl olduğunu anlatayım. Verdiğim sitedeki örnekten biraz daha farklı bir yol izledim, oradaki örnek hatalı gibi geldi ve bazı durumları atlayabiliyordu.

Kesme işlemi alt ve üst sınır için iki kere yapılıyor. her abc üçgen için abc üçgeni için 3 tane doğru parçamız var, ab bc ca. Her doğru parçası için şu algoritmayı uyguluyoruz.

  • Eğer her iki noktada doğru tarafta ise, ikinci noktayı al.
  • Birinci nokta doğru, ikincisi yanlış tarafta ise doğru parçasının sınır ile kesiştiği yeri al.
  • Birinci nokta yanlış, ikincisi doğru tarafta ise önce doğru parçasının sınır ile kesiştiği yerisonra ikinci noktayı al.
  • Her iki noktada dışarda ise hiç bir nokta alma.

Bu algoritma sonucu aldığımız noktalar üçgenin plane in doğru tarafında kalan kısmı olmuş oluyor. Mesela yukarıdaki resimde soldaki üçgen için

collision21Önce üst kısım için clip yapıyoruz. a dan b ye giderken her iki noktada doğru tarafta, sadece b alınıyor. b den c ye giderken b içerde c dışarıda bc doğru parçası ile sınırın kesiştiği yeri (bc’) alıyoruz. c den tekrar a ya giderken ilk nokta yanlış ikincisi doğru yerde olduğu için kesişim noktasını (ca’) ve sonra a yı alıyorız. sonuçta yeni oluşan şekil. b bc’ ca’ a dörtgeni oluyor. aynı işlemi bu sefer alt sınır için yapıyoruz ve sonuçta bc’ ca’ a b(bc’)’ ab’ beşgenini elde etmiş oluyoruz. Bu algoritma sonucu elimizde en iyi ihtimalle 0 nokta  (tüm noktalar dışarıda ise) en kötü ihtimallede bir beşgen oluşacak.

En alttaki resim algoritmanın güzel tarafını gösteriyor. Bütün polygonları kestikten sonra bu sefer y ekseni yönünde bakam bir kesit aldığınızı düşünün. Her şey iki boyuta iniyor ve silindirimiz bir çembere dönüşüyor. Eğer bu çember içinde kalan bir polygonumuz varsa bu onun silindir içinde kaldığını ve kamera ile çarğıştığını gösteriyor!

Peki 2 boyutlu düzlemde bir çember ve doğru parçasının (artık şekilleri doğru parçası array i olarka düşünelim =) ) kesiştiğini nasıl anlayacağız? Bunun için biraz vektör bilgisine ihtiyaç var. Sitede verilen örnek programın bu kısmı düzgün çalışıyor, açıklamasına şuradan bakabilirsiniz.

http://local.wasp.uwa.edu.au/~pbourke/geometry/pointline/

Burada farklı olan tek şey eğer doğru üzerindeki nokta doğru parçası dışında ise biz o noktaya yakın olan sınırı alıyoruz.

Eğer çemberimiz şekil ile kesişiyorsa kişiyi hareket ettirmek durumunda kalıyoruz. Burada iki ihtimal var. Ya üçgenimizin üzerine tırmanırız (eğer eğim uygun ise) veya silindiri üçgen ile kesişmiycek şekilde uzaklaştırırız.

collision31İkinci durum daha kolay olayı, iki boyutta düşünürek halledebiliyoruz. Eğer aradaki uzaklık a ise, çemberi r – a kadar hareket ettiriyoruz ve sorun çözülüyor.

collision4Birinci durumda (verdiğim sitede yeterli anlatılmamış, eksik kalmış gibime geldi) ise işler biraz daha karışık. Eğer üçgenin eğimi uygun ise üçgenin üzerine tırmanmamız gerekiyor.  Öncelikle çemberin kesişen nokta yönündeki uç noktayı (a boktası) buluyoruz. Amaç bu a noktasını yeterince yukarı kaldırmak böylece collision u engellemek. Bunun içinde üçgen üzerinde olan a’ noktasını bulmak lazım. Bunu bulmak içinde şu formülü kullandım.

http://gpwiki.org/index.php/MathGem:Height_of_a_Point_in_a_Triangle

Bu linkte procedure kısmındaki formül ile a’ noktasını buluyoruz. Bu nokta üçgen üzerinde ve a ile aynı x-z koordinatlarına sahip (formülde z ve y harflerini değiştirin, bizim aradığımız y). a’ noktasını bulduktan sonraa ile arasındaki yükseklik farkını buluyoruz ve silindirimizi o uzunlukta yukarı kaldırıyoruz.

Bütün sorunları bu şekilde çözemiyoruz malesef. Bir diğer problem ise tamamen yatay düzlemlerde oluşuyor. Mesela yüksek bir noktadan düştüğümüzü düşünün. Altımızda ise büyük bir üçgen var, bu üçgen bizim silindirimizin sınırlarına girdiğinde üstten görünüş şu oluyor.

collision5Burada dikkat ederseniz hiç bir doğru parçası çember ile kesişmiyor, ama yine de bir collision var. Bu durumu anlayabilmek için bir test daha gerekiyor. Bu testte çemberin merkezinin üçgen içinde mi değil mi onu arıyoruz. Bunun için abc üçgeni ve n noktasında her doğru parçası için merkez aynı tarafta mı kontrol ediyoruz. mesela ab doğru parçası için önce an vektörünü buluyoruz ve bunun dot product ını hesaplıyoruz, aynı işlemi bc ve ca için de yapıyoruz. Eğer bütün dot product lar pozitif ise nokta çemberin içinde demek oluyor. Bu durumda yine aynı şekilde silindiri bir parça yukarı kaldırarak sorunu çözüyoruz. (şurada ayrıntı açıklama var http://www.blackpawn.com/texts/pointinpoly/default.html)

Ama maalesef bu da yeterli olmuyor =) Bir diğer (ve oldukça büyük bir sorun) ise eğer çok hızlı hareket ediyorsak ne olacağı. Bu durumu henüz programa eklemedim ama şu şekilde çözülebilir. Önceki koordinatımızdan yeni koordinata bir doğru parçası çizdiğimizde eğer bu doğru parçası polygon ile kesişiyorsa collision oluyor demektir. Ama bu tam yeterli bir çözüm değil o yüzden henüz eklemek istemedim. Aklıma daha iyi bir çözüm geldiğinde onu eklemeye çalışacağım.

Programın son hali

Kaynak dosyaları

(ek: f tuşunu basılı tutarak uçabiliyorsunuz =D)

Kağıt üzerinde kod

Posted on by

Evrimsel algoritmalar dersine giren hocamızın bir isteği olmuştu, ilk duyduğumda baya garipsemiştim. Proje kodunun yazılı çıktısını istemişti. Yani o zaman ne kadar saçma bir şey diye düşündüm ama şimdi aslında bir parça mantıklı geliyor.

Yani mesela ben oturup bir program yazarken (daha doğrusu yazmadan önce) uzun süre problem üzerinde düşünmeyi severim. Bu düşünme sürecinden sonrada bir kerede (eğer büyük bir şey değilse) yazmaya çalışırım. Zaten olabilecek hataları kafamdan bulabildiğim için yazma süreci nispeten hatasız olur (yani algoritma olarak hatasız, yoksa hala bol bol yazım hatası yaparım =D). Eğer bir problemle karşılaşırsam düşünme evresine geri dönerim.

Yani böyle bir durum için ideal olabilir, eğer bir başkasının kodunu inceleyeceksem (hele buda proje gibi büyük bir şey ise) çıktı almak iyi bir fikir olabilir. Mesela operating system design projesinde az zaman harcamadım ekran başında o kernel kodlarını çözmek için.

Şimdi projeyi çıktı alınabilir uygun bir formata sokmaya çabalıyordum oradan aklıma geldi =)

Evrimsel algoritmalar projeside bir parça yalan oldu gibi. Şu an nispeten çok daha kısa sürelerde (1 saat ^^) 25 milyona kadar iniyor fitness değerlerim ama ondan sonra çok yavaşlıyor. 1-2 gün beklerse heral 20 milyonu bulacak ama bir noktadan sonra dahada ineceğini sanmıyorum. Yani sonuçta az sayıda ki üçgenlerle ne kadar elde edilebilir bir resim bilemiyorum.

Bir çözüm yolu resmi parça parça oluşturmak olabilir. Önce tüm resim için algoritma çalışır ve bir anahat görüntüsü elde edilir. Sonra daha ufak parçaları oluşturmaya çalışırız, bu anahat resmi de arkada kalır. Bu parçalar gittike küçültülür ve sonunda düzgün bir resim elde edilir. Ama üçgen sayısı kaça çıkar bilemiyorum. Tahminimce 1024 üçgen yeterli olacaktır, buda 72 kb anlamına geliyor. Orjinal 512×512 resim 768kb ki arada ciddi fark.

Odtü programlama yarışması 2009

Posted on by

http://www.cclub.metu.edu.tr/yarisma/2009/

sonuclar Finalistler açıklanmış, bu sene de odtü ye gidiyoruz bakalım ^^ Geçen senenin aksine iyi bir grup kurduk bakalım umutluyuz ama oraya gidince durumlar nasıl olacak.

Doğrusu öneleme sorularını biraz özensiz bulmuştum. Geçen sene ki neredeyse bütün sorular bir cinlik gerektiriyordu, bu sene ise 6 sorudan 3 ü çok basit bir biçimde çözülebiliyor. 1 tanesi ise verilen kısıtlamalarla çözülebilir gibime gelmedi. Diğer iki sorudan birisi baya meşhur bir problem, google da arama yapılınca çözüm yardım alınabilecek bir şeydi. Doğrusu tek bir soru benim hoşuma gitti =)

Eski Odtü algoritma yarışması sorusu

Posted on by

Geçen yıl finalde sorulan sourlardan birisi o zamandan beri aklıma bir parça takılmıştır. Bir türlü nasip olmadı oturup uğraşmak.

Odtü lü arkadaşların soru için güzel bir hikayesi vardı, şimdi aklımda değil malesef.

Soruda bir input dosyasından dikdörtgen koordinatları okuyoruz (her dikdörtgen için sol-üst ve sağ alt köşenin koordinatları veriliyor). İstenen ise bu dikdörtgenleri tek renk bir kalem ile bir kağıda çizer ve boyar isek oluşan şeklin alanı.

Dikdörtgenlerin boyutlarunda ve koordinatlarında sınır olmadığı için (integer sınırlarında farzedin) “İki boyutlu bir array açayım, dikdörtgen olan yerleri 1 yapayım” gibi bir mantık işe yaramıyor.

Aklıma gelen bir çözüm yolu (ki obvious çözüm gibi bir şey) her yeni eklenen dikdörtgeni öncekiler ile karşılaştırmak ve eğer kesişiyorsa önceki dikdörtgeni kesişmeyen iki dikdörtgene bölmek. Örnek resim:

res11

Mesela soldaki örnekte b dikdörtgeni önceden gelmiş bir dökdörtgen. a ise yeni gelen dikdörtgen. Biz bu b yi şu şekilde ikiye bölüyoruz (Yazının bu kısmında l4d oynamak için ufak bir ara verdim, herkese tavsiye ederim bu oyunu =p)

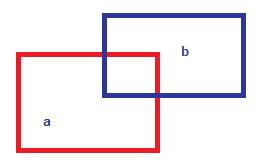
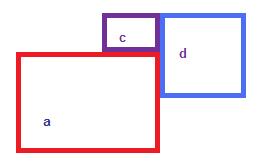res2b dikdörtgenini c ve d olarak ikiye ayırdık. Artık kesişme sorunu yok ve alan olarakta aynı alan. Elbette farklı şekilde de bölünebilirdi.

Bu bölme işleminden sonra a yı kalan dikdörtgenlerle (eğer kaldıysa) kontrol edeceğiz. Gerekirse yine aynı şekilde onları da böleceğiz. Her çakışma sonucu ikiye bölünecek diye bir şart yok. Eğer şanslı isek eski dikdörtgen yenisini kapsar ve daha fazla kontrole gerek kalmaz. Veya mesela şu örnek için:

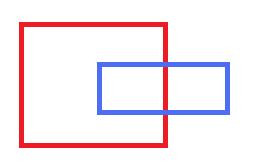res3Eğer yeni gelen dikdörtgen kırmızı olan ise sadece mavi dikdörtgenin kırmızı içinde kalan kısımlarını çıkartarak (mavi dökdörtgeni bir parça sol tarafından kırparak) çakışmadan kurtulabilirdik. Eğer yeni gelen mavi olan ise ve kırmızıyı bölmeye kalkarsa üçe bölmek zorunda kalacaktık. Bunun yerine algoritmayı biraz değiştirerek yine aynı şekilde maviyi (yeni gelen dikdörgeni) kırparak dikdörtgen sayısını azaltabiliriz. Yine aynı şekilde yeni gelen dikdörtgen eskini kapsıyor ise eskisini listeden çıkartabiliriz, bu durumda hala yeni dikdörtgeni kontrol etmek zorundayız ama en azından toplam dikdörtgen sayımız azaldı.

Yani en kötü ihtimalle her karşılaştırma için bir yeni dikdörtgen oluşturuyoruz. Aklıma gelen şu anlık tek çözüm bu, ama performansı konusunda şüphelerim var. Yani mesela n dikdörgen var ise, n+1 inciyi eklerken her karşılaştırma için 1 artar ise toplamda 2n+1 dikdörtgen olacak. Tabi bu çok uç bir input ve muhtemelen tek bir input dosyası içinde sayısının fazla olması imkansız. Alan hesaplamak içinde en sonunda tek tek bütün dikdörtgenlerin alanlarını toplayacağız.

Son zamanlarda da asıl aklıma takılan böyle bir algoritmanın complexity si ne olur. Yani bir kere O(n^2) den düşük olamayacak (sonuçta her yeni geleni bir öncekilerle kontrol ediyoruz). Ama devamlı dikdörtgenler bölüneceği için n^2 den yüksek bir complexity alması lazım gibi duruyor.

Yapılabilecek başka bir iyileştirme ise dikdörtgenleri sort sağ noktasının x koordinatlarına göre sort edilmiş şekilde tutmak. Eğer yeni dikdörtgenin sol noktasının x koordinatı, eskilerin sağ x ini geçer ise artık kalan dikdörtgenleri kontrol etmeye gerek kalmayacak. Eğer sorted bir şekilde tutar isek dikdörtgenleri linked list yapısında saklamak daha mantıklı çünkü bölünen yeni dikdörtgenler (ve yeni gelen dikdörtgenler) devamlı araya girmeye kalktığında array i shift etme zorluğu yaşamayalım. Bu ayrıntıyıda algoritmaya eklersek bariz bir şekilde iyileştirme sağlayacaktır (eğer bölünme olmasaydı O(nlogn) olacaktı, ama tabi gerçek complexity yi hesaplamak çok daha fazla karıştı =D).

Bu sorunun ikinci kısmı ise çevre hesaplamak idi (sadece şeklin etrafını çevreleyen değil, içerde boşluk varsa o boşluğunda çevresi de hesaba katılacak). Çevrenin tek farkı ise şu. Önce yine aynı şekilde dikdörtgenler kesişmeyecek şekilde oluşturacağız. Sonra her dikdörtgenin çevresini bir toplam çevre değerine ekleyeceğz. Daha sonra, dikdörtgeni bir önceki dikdörtgenler ile karşılaştıracağız, eğer iki dikdörtgen teğet ise ne kadar uzunlukta teğet olduğunu bulacağız ve o değerinin iki katını toplamdan çıkaracağız.

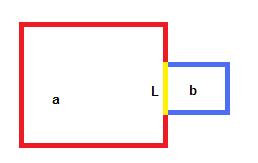res4 Mesela a ve b nin çevreleri A, B ise ve sarı çizginin (teğet olan kısım) uzunluğu L ise toplam çevre.

Çevre = A + B – 2*L

olacak.

Henüz daha iyi bir çözüm aklıma gelmedi, olabilir diye umuyorum. Algoritmayı koda dökmeye hep üşeniyorum. Çok fazla ağır gibi durmasada iki dikdörtgenin karşılaştırılması ve bölünmesi baya zor olacak gibi duruyor, bir çok ihtimal var sonuçta. Belki daha iyi bir tane bulunabilir bilmiyorum. Odtü finalinde çok kötü bir algoritma yazmıştım, kesişen her iki dikdörtgen için kesişen alanı çıkarıyordu. Ama mesela 3 dikdörtgen aynı noktada kesişirse o durumda patlıyordu. Belki bu algoritma biraz geliştirilerek doğru sonuç verecek bir şeye çevrilebilir belli olmaz.

shultays.com/blog

Posted on by

Word press in tema düzenlemeye izin vermediğini farkedinci blog u taşıma kararı verdim. Bir süre ikisinde de yazacağım aynı yazıları daha sonra tamamen diğerine geçiş yapmayı düşünüyorum.

http://www.shultays.com/blog

şu anlık sub domain almadım, zaten server ı bedavaya veren bir arkadaş olduğu için utanıyorum daha fazla istek yapmaya 🙂

Ayrıca aklıma yeni bir proje geldi, blog postlarını mysql den okuyup shultays.com da gezegen olarak göstereceğim. gezegene tıklayınca javascript ile alakalı post u pop up olarak açacak. Eğer düzgün gösterebiliyorsa direk flash içinde de göstermeyi deneyebilirim ama flash ın html yorumlaması çok sınırlı olduğu için ne kadar iyi olacak bilmiyorum (zaten code taglarını gösteremeyecek, alıntılar görünmeyecek bir acayip olacak yatacak herhalde o fikir)

Hatta commentleri bile gezegenin etrafında dönen uydular gibi yapabilirim =D.  Bir evrende en fazla diyelimki 20 gezegen göstersin istiyorum, 20 den fazla post var ise aşağıda sayfa numarasına tıklayacağız, tıklayınca çok hızlı bir şekilde uzaklaşacak o evrenden ve “yeni” bir evrene geçecek. Bir gezegene tıklayınca yanına gidip alakalı sayfayı becerebilirsem sayfayı flash ta gösterecek ve commentler uydumuz olacak, olmaz ise alakalalı sayfayı pop-up olarak açacak.

Bakalım fikir güzel, eğer yapabilirsem sitenin flash ve php dosyalarını açabilirim. Şimdiye kadar pek açacak bir şey yoktu o yüzden açmamıştım =)

pff

Posted on by

1 hafta tatil, çok fazla iş, pek az istek.

Kimse düşmesin böyle bir duruma. En azından ‘tatil’imiz var diye sevineyim.

shultays.com

Posted on by

shultays.com

Bir yıl kadar önce yaptığım, 3D grafik olayına giriş yaptığım kişisel web sitem. Hazırlık-1.sınıf zamanlarında AS2 olarak başlamıştım, daha sonra AS3 kullanmaya başladım. Asıl amacım flashta 3D site yapmak değilde bir 3D grafik motoru yazmak idi, bu yüzden hiç bir hazır kütüphane kullanmadım. AS2 hali hala duruyor, ama resimler eksik, mesela ortada bir küp vardı o görünmüyor, kenarda bir Otostopçunun Galaksi Rehberi vardı, hatta kapağı bile açılıyordu (vay be)

Pek kullanıcı dostu değil, zaten öyle olması için de tasarlanmadı =p Aslında aklımda göze güzel gelebilecek bir menü sistemi var ama hep üşeniyorum. Uzun süredir de flash kullanmadım, o yüzden de biraz çekinme var. Hem zaten zaman da yok =D

WASD tuşları ile kamera aşağı yukarı hareket ediyor. İleri gitmek için RF tuşlarını kullanarak ileri geri gidebilirsiniz. QE ekranı çevirir. Ayrıca farenin sol tuşunu basılı tutarakta kamerayı döndürebilirsiniz.

Renkli ve ünlemli gezegenler aslında bizim linklerimiz oluyor, onlara tıklayınca gezegene gidiyoruz ve onunla alakalı flash yükleniyor. Beyaz gezegenler de boş gezegenler, yanlarına gidebiliyorsunuz ama bir şey açmıyorlar.

Hayalimdeki proje evrende kişilere belirli bölgeler vermek, o bölgelerde kendi gezegenlerini oluşturmalarını sağlamak idi. Siz evrende gezinerek aslında siteler arasında geziniyor gibi olacaktınız. Lakin bir süre sonra artık sıkmaya başladı ve bitirilmemiş projeler arasında yerini aldı. Bir diğeride bu mesela. Multiplayer bir savaşlı yarışlı oyun yapayım dedim ama görebileceğiniz o daha başlarda yalan oldu =)

Aradığım mutluluğu açık kaynakta buldum

Posted on by

İlk açık kaynak kodumu yayınlıyorum, buyrunuz:

[sourcecode language=’cpp’]
unsigned int tay[] = {2942066556, 2959137644, 2193827523, 2210048174, 2501139473, 2398640398, 2147848541, 0};
unsigned int *t = ((unsigned int*)tay)+1, a=0, y=0;
char yat[24]={0};

while(*t){
printf(“%c”, yat[y++]=*t&1?*tay>>(*t>>1&3)*8&127:32);
t+=(*t>>=*t&1?3:1)&~7?0:1;
a++-22?0:printf(“%sn”, yat,y=a=0);
}[/sourcecode]

(bu kod hakikaten çalışıyor, hatta güzel bir output u var söyleyeyim =))