Geçen yıl finalde sorulan sourlardan birisi o zamandan beri aklıma bir parça takılmıştır. Bir türlü nasip olmadı oturup uğraşmak.
Odtü lü arkadaşların soru için güzel bir hikayesi vardı, şimdi aklımda değil malesef.
Soruda bir input dosyasından dikdörtgen koordinatları okuyoruz (her dikdörtgen için sol-üst ve sağ alt köşenin koordinatları veriliyor). İstenen ise bu dikdörtgenleri tek renk bir kalem ile bir kağıda çizer ve boyar isek oluşan şeklin alanı.
Dikdörtgenlerin boyutlarunda ve koordinatlarında sınır olmadığı için (integer sınırlarında farzedin) “İki boyutlu bir array açayım, dikdörtgen olan yerleri 1 yapayım” gibi bir mantık işe yaramıyor.
Aklıma gelen bir çözüm yolu (ki obvious çözüm gibi bir şey) her yeni eklenen dikdörtgeni öncekiler ile karşılaştırmak ve eğer kesişiyorsa önceki dikdörtgeni kesişmeyen iki dikdörtgene bölmek. Örnek resim:
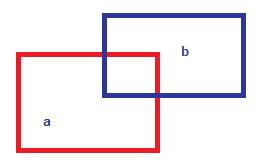
Mesela soldaki örnekte b dikdörtgeni önceden gelmiş bir dökdörtgen. a ise yeni gelen dikdörtgen. Biz bu b yi şu şekilde ikiye bölüyoruz (Yazının bu kısmında l4d oynamak için ufak bir ara verdim, herkese tavsiye ederim bu oyunu =p)
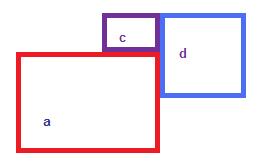b dikdörtgenini c ve d olarak ikiye ayırdık. Artık kesişme sorunu yok ve alan olarakta aynı alan. Elbette farklı şekilde de bölünebilirdi.
Bu bölme işleminden sonra a yı kalan dikdörtgenlerle (eğer kaldıysa) kontrol edeceğiz. Gerekirse yine aynı şekilde onları da böleceğiz. Her çakışma sonucu ikiye bölünecek diye bir şart yok. Eğer şanslı isek eski dikdörtgen yenisini kapsar ve daha fazla kontrole gerek kalmaz. Veya mesela şu örnek için:
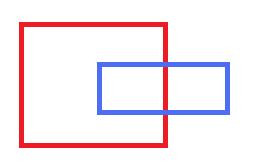Eğer yeni gelen dikdörtgen kırmızı olan ise sadece mavi dikdörtgenin kırmızı içinde kalan kısımlarını çıkartarak (mavi dökdörtgeni bir parça sol tarafından kırparak) çakışmadan kurtulabilirdik. Eğer yeni gelen mavi olan ise ve kırmızıyı bölmeye kalkarsa üçe bölmek zorunda kalacaktık. Bunun yerine algoritmayı biraz değiştirerek yine aynı şekilde maviyi (yeni gelen dikdörgeni) kırparak dikdörtgen sayısını azaltabiliriz. Yine aynı şekilde yeni gelen dikdörtgen eskini kapsıyor ise eskisini listeden çıkartabiliriz, bu durumda hala yeni dikdörtgeni kontrol etmek zorundayız ama en azından toplam dikdörtgen sayımız azaldı.
Yani en kötü ihtimalle her karşılaştırma için bir yeni dikdörtgen oluşturuyoruz. Aklıma gelen şu anlık tek çözüm bu, ama performansı konusunda şüphelerim var. Yani mesela n dikdörgen var ise, n+1 inciyi eklerken her karşılaştırma için 1 artar ise toplamda 2n+1 dikdörtgen olacak. Tabi bu çok uç bir input ve muhtemelen tek bir input dosyası içinde sayısının fazla olması imkansız. Alan hesaplamak içinde en sonunda tek tek bütün dikdörtgenlerin alanlarını toplayacağız.
Son zamanlarda da asıl aklıma takılan böyle bir algoritmanın complexity si ne olur. Yani bir kere O(n^2) den düşük olamayacak (sonuçta her yeni geleni bir öncekilerle kontrol ediyoruz). Ama devamlı dikdörtgenler bölüneceği için n^2 den yüksek bir complexity alması lazım gibi duruyor.
Yapılabilecek başka bir iyileştirme ise dikdörtgenleri sort sağ noktasının x koordinatlarına göre sort edilmiş şekilde tutmak. Eğer yeni dikdörtgenin sol noktasının x koordinatı, eskilerin sağ x ini geçer ise artık kalan dikdörtgenleri kontrol etmeye gerek kalmayacak. Eğer sorted bir şekilde tutar isek dikdörtgenleri linked list yapısında saklamak daha mantıklı çünkü bölünen yeni dikdörtgenler (ve yeni gelen dikdörtgenler) devamlı araya girmeye kalktığında array i shift etme zorluğu yaşamayalım. Bu ayrıntıyıda algoritmaya eklersek bariz bir şekilde iyileştirme sağlayacaktır (eğer bölünme olmasaydı O(nlogn) olacaktı, ama tabi gerçek complexity yi hesaplamak çok daha fazla karıştı =D).
Bu sorunun ikinci kısmı ise çevre hesaplamak idi (sadece şeklin etrafını çevreleyen değil, içerde boşluk varsa o boşluğunda çevresi de hesaba katılacak). Çevrenin tek farkı ise şu. Önce yine aynı şekilde dikdörtgenler kesişmeyecek şekilde oluşturacağız. Sonra her dikdörtgenin çevresini bir toplam çevre değerine ekleyeceğz. Daha sonra, dikdörtgeni bir önceki dikdörtgenler ile karşılaştıracağız, eğer iki dikdörtgen teğet ise ne kadar uzunlukta teğet olduğunu bulacağız ve o değerinin iki katını toplamdan çıkaracağız.
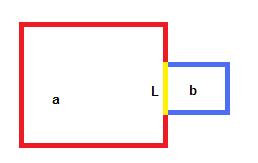Mesela a ve b nin çevreleri A, B ise ve sarı çizginin (teğet olan kısım) uzunluğu L ise toplam çevre.
Çevre = A + B – 2*L
olacak.
Henüz daha iyi bir çözüm aklıma gelmedi, olabilir diye umuyorum. Algoritmayı koda dökmeye hep üşeniyorum. Çok fazla ağır gibi durmasada iki dikdörtgenin karşılaştırılması ve bölünmesi baya zor olacak gibi duruyor, bir çok ihtimal var sonuçta. Belki daha iyi bir tane bulunabilir bilmiyorum. Odtü finalinde çok kötü bir algoritma yazmıştım, kesişen her iki dikdörtgen için kesişen alanı çıkarıyordu. Ama mesela 3 dikdörtgen aynı noktada kesişirse o durumda patlıyordu. Belki bu algoritma biraz geliştirilerek doğru sonuç verecek bir şeye çevrilebilir belli olmaz.
